1. 简述
论文题目:《CONTINUOUS CONTROL WITH DEEP REINFORCEMENT
LEARNING》。该论文提出了基于 deterministic policy gradient 的 DDPG(deep deterministic policy gradient) 算法,能够运用在连续的动作空间中,能够 learn policy “end to end”。
1.1 处理连续动作空间的问题
DQN存在的问题是只能处理低维度,离散的动作空间。
不能直接把Q-learning用在连续的动作空间中。因为Q-learning需要在每一次迭代中寻找最优的$a_t$。对于参数空间很大并且不受约束的近似函数和动作空间,寻找最优的$a_t$是非常非常慢的。
连续动作空间的离散化:离散化后的动作数量随着自由度呈指数增长,导致离散后的动作空间太大,很难进行有效地探索。而且过于稀疏的离散化抛弃了动作空间的本身的结构信息。
1.2 处理庞大状态空间的问题
- 非线性函数逼近器(例如神经网络)的收敛性无法保证,但是这种形式的函数逼近器对于庞大的状态空间的学习和泛化而言是必要的。
1.2 DDPG 的关键点
model-free, off-policy, actor-critic, using deep function approximators
based on the the deterministic policy gradient (DPG) algorithm (Silver et al., 2014)
借鉴DQN两个重要技巧,对神经网络表示的value functions进行学习:
the network is trained off-policy with samples from a replay buffer to minimize correlations between samples.
the network is trained with a target Q network to give consistent targets during temporal difference backups.
use batch normalization (Ioffe & Szegedy, 2015)
DDPG的优点在于它的简洁,只需要actor-critic框架和简单的学习算法,能够在实际的控制问题上发挥优势,比需要很多动力学建模的规划算法效果好。
2. 相关知识
重点是目标函数,动作-值函数以及它的贝尔曼方程(迭代形式),Q-learning算法(即off-policy方法,行动策略和目标策略不是同一种策略)。
2.1 符号定义
t 时刻观测值: $\boldsymbol{x_t}$
假定环境完全可知,t 时刻状态值: $\boldsymbol{s_t} = \boldsymbol{x_t}$
t 时刻动作: $\boldsymbol{a_t} \in \mathbb{R}^N $
奖励值: $r_t$,标量
动作策略: $\pi : \mathcal{S} \rightarrow \mathcal{P}(\mathcal{A})$
初始状态分布: $p(s_1)$
状态转移概率: $p(s_{t+1} | s_t, a_t)$
奖励函数: $r(s_t, a_t)$
2.2 公式定义
折扣奖励函数: $R_t = \sum_{i=t}^T \gamma ^ {i - t} r(s_i, a_i)$, $\gamma \in [0, 1]$
折扣状态访问分布: $\rho^\pi(s’) := \int_{\mathcal{S}} \sum_{t=1}^\infty \gamma^{t-1} p_1(s) p(s \rightarrow s’, t, \pi) ds$
目标函数: $J(\pi_\theta) = \int_\mathcal{S} \rho^{\pi}(s) \int_{\mathcal{A}} \pi_\theta(s, a) R_1(s, a) da ds =
\mathbb{E}_{s_i \sim \rho^\pi, a_i \sim \pi}[R_1]$动作-值函数: $Q^{\pi}(s_t, a_t) = \mathbb{E}_{s_{i \gt t} \sim \rho^\pi, a_{i \gt t} \sim \pi}[R_t | s_t, a_t]$
动作-值函数的贝尔曼方程(迭代形式): $Q^\pi(s_t, a_t)=\mathbb{E}_{s_{t+1} \sim \rho^\pi} \left[r(s_t, a_t) + \gamma \mathbb{E}_{a_{t+1} \sim \pi} [Q^\pi (s_{t+1}, a_{t+1})] \right]$
如果动作策略是确定性策略,表示为 $\mu : \mathcal{S} \rightarrow \mathcal{A}$,则动作-值函数的贝尔曼方程的形式为:假设用参数 $\theta^Q$ 去逼近动作-值函数并采用Q-learning,则定义损失函数如下:
注意虽然$y_t$中也含有$\theta^Q$,但是对$L(\theta^Q)$求梯度时,通常忽略$y_t$,不对其求导。
3. 算法
DDPG算法基于DPG算法,并采纳DQN中的两个重要技巧。接下来简单介绍一下基础算法DPG。
3.1 DPG算法
DPG算法采用确定性策略 $\mu(s | \theta^\mu)$,每一时刻都将状态映射成确定的动作,同时也采用actor-critic框架。critic用参数为$\theta^Q$的函数 $Q(s,a|\theta^Q)$表示,并通过Q-learning和贝尔曼方程的方式进行学习。actor对目标函数应用链式法则(即策略梯度)更新参数 $\theta^\mu$:
Q-learning采用的是异策略,行动策略表示为 $\beta$,目标策略表示为 $\mu$。 上述目标函数中,最外层是关于状态 $s_t$ 分布的平均,$s_t$ 就是通过执行 $\beta$ 策略采样来的。但是最里层动作-值函数如果展开成贝尔曼方程的形式,下一时刻采用的动作策略则是 $\mu$,如2.2节的第六条公式。
DPG 采用 SGD 随机梯度更新规则。采用批梯度下降是很难收敛的。
3.2 DDPG算法
绝大多数优化算法都是假设样本是独立且均匀分布的,但是强化学习采集的样本本身就是一个序列,所以相邻间的样本是有关联的,不满足假设条件。另外,通常是采用mini-batch更新的方式,而不是在线更新。
为了解决样本相互关联的问题,DQN采用了经验回放池,具有固定大小,存储每次探索的 $(s_t, a_t, r_t, s_{t+1})$。当经验回放池满了之后,会丢弃最旧的数据,增加新采样数据。每次更新的时候,actor和critic都会统一从经验回放池中抽取一个mini-batch进行更新。经验回放池可以尽可能地设置得大一点,这样每次抽取的样本关联度会降低。
如果直接按照2.2节的第七条公式去更新网络 $Q(s, a|\theta^Q)$,在大多数环境中都是会发散的。因为该公式的计算目标值 $y_t$ 时也用了网络 $Q(s, a|\theta^Q)$ 的值。很明显,这个网络在还没有收敛的时候,作为目标的一部分进行学习,结果很容易发散。因为目标本身就好像在追求一个不稳定的值。
为了避免目标Q值 $y_t$ 中包含不稳定的网络 $Q(s, a|\theta^Q)$ 输出,采用称为“soft target update” 的更新方法。首先,重新复制一份actor网络,$\mu’(s|\theta^{\mu’})$和critic网络,$Q’(s, a|\theta^{Q’})$,它们用来计算目标Q值。目标网络 $\mu’(s|\theta^{\mu’})$ 和 $Q’(s, a|\theta^{Q’})$ 随着学习网络 $\mu(s|\theta^{\mu})$ 和 $Q(s, a|\theta^Q)$ 更新而更新,但是目标网络的更新幅度远小于学习网络: $\theta’ \leftarrow \tau \theta + (1 - \tau) \theta$, $\tau \ll 1$。这意味着目标网络变化缓慢,提高了目标值计算的稳定性。(不过应该没有彻底解决这一问题,毕竟还是目标网络用于目标值计算时也并非稳定的,只是变化缓慢而已。)但是降低目标网络的更新幅度,可能会让学习网络的更新变慢,也就是牺牲更新速度来提供收敛稳定性。不过文中提到,在实际中,学习的稳定性比学习的速度要重要得多。
另一个问题就是观测值包含不同元素(例如位置信息和速度信息),这些元素包含不一样的物理量度,变化值范围不同,如果采用这些不同量度的元素,可能会导致网络学习效率变低,也很难在不同环境中泛化。因此需要将所有这些元素重新归一化到相同的范围。采用的方法是Ioffe 和 Szegedy 提出的batch normalization。这种方法会将每个mini-batch中的样本每个维度归一到相同的均值和方差。同时保留这个均值和方差,以用于测试的样本的归一化。对 $\mu$ 网络和 Q 网络的所有隐藏层和状态输入都进行归一化。
为了提高探索效率,采用的行动策略 $\mu’$是对目标策略 $\mu(s_t|\theta_t^\mu)$加上噪声 $\mathcal{N}$:
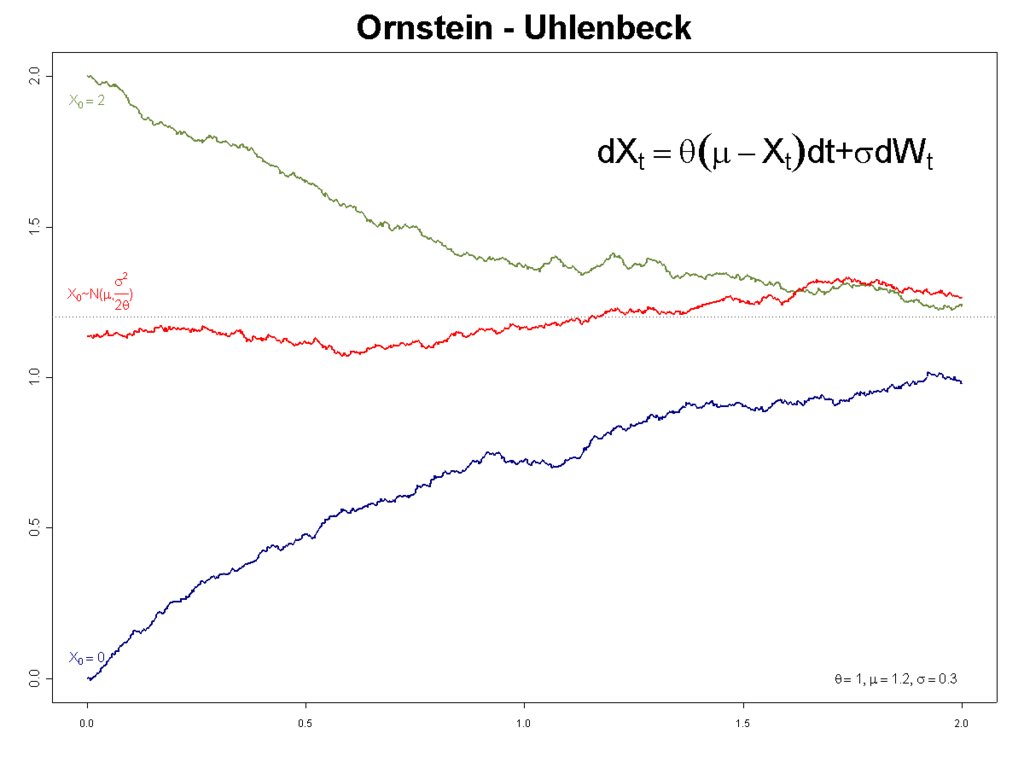
$\mu’(s_t) = \mu(s_t|\theta_t^\mu) + \mathcal{N}$。论文中采用的噪声是Ornstein-Unlenbeck process(O-U过程)。