论文题目:Prioritized Experience Replay
1. 论文简述
在 Nature DQN 和 Double DQN 论文中经验回放池的采样是基于均匀分布采样,一种更合理的方式应该考虑这些经验中哪些更具有对训练更有价值,也就是给这些经验值分配不同的优先级权重,在采样时这些重要的经验被抽取的概率对更大。DQN 论文中提及很早之前有研究做过一种 “Prioritized sweeping” 方法,就是实现经验回放的不均匀采样。本篇论文在前人的研究基础上提出一种新的框架——优先经验回放,使优先级更大的经验被选中的几率更大。“DQN + 优先经验回放”的方法在 Atari 游戏的测试中比 “DQN + 均匀经验回放”的方法更好(49个游戏有41个性能更优越)。
1.1 优先经验回放简述
在线强化学习利用每次获得的经验流 $(s_t, a_t, r_t, s_{t+1})$ 来更新参数。最简单的更新方式就是每次获得一个经验流,在进行一次更新后就抛弃。这样做有两个问题:
由于状态之间存在关联,因此用来更新的经验值并非是独立的,这破坏了很多算法模型的独立性假设。
有些经验是十分罕见和宝贵的,有可能下一次学习还需要继续用到,因此直接丢弃是不理智的。
采用经验回放的方法可以减少需要用于训练的经验,加快训练,同时牺牲一些计算资源和存储资源来减少智能体和环境的交互。对于强化学习智能体而言,计算资源、存储资源和环境交互的次数相比,是一种 cheaper 资源。
优先经验回放背后的关键思想是有些经验在用于智能体的学习时会比另外一些经验更有意义。另外,有些经验可能在当前对于智能体的学习并不是很有帮助,但是在智能体能力提升之后,可能对智能体的学习会增加。
优先经验回放用 TD 误差的大小来衡量哪些经验对学习过程具有更大的贡献。但是使用优先经验回放会带来一点多样性的损失和引入偏差。本文引入随机优先 (stochastic prioritization) 来缓解多样性损失的问题,并通过重要性采样来纠正偏差。
优先经验回放的可以对每一个 transition(RL 中交互的原子单位,以下称为“经验”)计算优先级指标,也可以对一个经验序列计算优先级指标。
1.2 相关知识
1993 年 Moore 和 Atkeson 等人就提出了 “prioritized sweeping” 的概念,根据状态更新后的变化值来对每个状态进行排序,优先选出更新后最优的状态。 但是这种方法只适用于有模型的强化学习问题。本文提出的优先经验回放是用在无模型的强化学习问题上,另外本文还新采用了两个技巧——随机优先方法 (stochastic prioritization) 和 重要性采样。
TD 误差其实提供了一种更新后的变化值的描述。在Q网络中,TD 误差就是目标 Q 网络计算的目标 Q 值和在线 Q 网络计算的 Q 值之间的差距。注意到在经验回放池里面的不同的样本由于 TD 误差的不同,对我们反向传播的作用是不一样的。TD 误差越大,那么对我们反向传播的作用越大。而TD 误差小的样本,由于TD 误差小,对反向梯度的计算影响不大。
2. 算法模型
2.1 衡量经验优先级的标准
优先经验回放最重要的部分是衡量每个经验优先级的标准。本文提出的第一种方法就是使用 TD 误差 来衡量经验的优先级。 TD 误差是指下一次更新后值的变化,如果 TD 误差大,说明用来更新的经验值具备更多的信息,因此优先级也更高。不过这种方法在一些环境下并不适用,那就是当奖励值是带有噪声的情况下。论文后面也讨论了其他衡量经验优先级的标准,目前先假定这种标准就是 TD 误差。
算法会将上一次计算的 TD 误差连同用于更新的经验共同存入经验回放池。如果是新的经验,并不知道其对应的 TD 误差,算法会给予这种经验最高的优先级,保证所有的经验都至少被回放一遍。
2.2 随机优先方法 (Stochastic prioritization)
每次都抽取 TD 误差最大的那个经验的经验回放方法称之为贪婪经验回放方法 (greedy TD-error prioritization)。这种方法有以下三个问题:
一般为了减少遍历经验回放池的巨大时间代价,每次只会对被抽取的经验更新它的 TD 误差值。也就是说如果一个经验一开始它的 TD 误差值很小,那么可能很长时间内都不会回放这个经验。
对噪声脉冲十分敏感(也就是比较随机的奖励值),逼近目标函数的误差也会加重这种算法的不稳定性。
贪婪经验回放会只专注于一小部分初始 TD 误差值比较高的经验,导致缺乏多样性,系统会过拟合。
为了解决贪婪经验回放存在的若干问题,本文引入了随机优先经验回放的方法,是均匀经验回放和贪婪经验回放两种方法的折衷。随机优先经验回放让经验池中每个经验被抽中的概率与它们的 TD 误差值呈现单调关系,但是也保证对于低优先级的经验同样会有非零的概率被抽中。对于经验 $i$,被抽中的概率表示如下:
其中 $p_i > 0$ 表示经验 $i$ 的优先级,指数 $\alpha$ 表示依赖优先级进行经验回放的程度,如果 $\alpha=0$,表示均匀经验回放。对于 $p_i$ 的定义,本文给出两种方法(实际应用大部分都使用第一种定义):
$p_i = |\delta_i| + \epsilon$,其中 $\epsilon$ 是一个正的常数,防止经验 $i$ 的 初始TD 误差值为0。
$p_i = \frac{1}{rank(i)}$,其中 $rank(i)$ 是根据 $|\delta_i|$ 的排名。
为了提高采样效率,采样的时间复杂度不能和经验回放池的大小 $N$ 成正比。对于第一种方法,采用基于 “sum-tree” 数据结构实现,采样和更新的时间复杂度是 $O(log N)$。对于第二种方法,采用二进制堆构建的优先队列,采样的时间复杂度为 $O(1)$,更新的时间复杂度为 $O(log N)$。
采样时,采用 $k$ 段概率相等的分段线性函数来近似经验的累积密度函数,采样时先根据概率抽取一段经验序列,再从一段经验中均匀随机抽取一个经验。如果是采用mini-batch的梯度优化方法,可以将 minibatch 的大小设置为 $k$,然后从每段经验序列中都抽取一个经验。
2.3 偏差补偿(偏差纠正)
引入随机优先级概念后,仍然会存在问题。注意到,如果是通过正常的经验重放,则使用随机更新规则。因此,对经验进行抽样的方式必须与它们的原始分布相匹配。如果采用的是均匀经验回放,那么采样的方法也相应是随机采样,这样每个经验都会有同等的概率被抽到,因而不会引入偏差。
但是如果采用了优先经验回放,就需要采用优先级采样而抛弃随机采样,这样就会向高优先级的样本引入偏差(即更高概率被抽中)。这种情况下,更新模型权重会有过拟合的风险。与低优先级经验相比,具有高优先级的经验样本可能多次用于训练。因此,模型只会使用一小部分经验更新权重。
为了纠正这种偏差,可以使用重要性采样 (importance-sampling),通过减少常见样本的权重来调整更新模型。 来纠正这种偏差:
注意公式中 $P(i)$ 才是经验 $i$ 被抽取的概率,$\frac{1}{P(i)}$ 是它的倒数。$\beta$ 的作用是控制这些重要性采样权重对学习的影响程度。在实际运用中,$\beta$ 参数在训练过程中会逐步上升到 1。随着 $\beta$ 的提高,上述公式对高优先级的样本的权重几乎不更新,而对低优先级的样本的权重进行较大的提升。因为当后期动作-值 Q 开始收敛时,无偏性的更新对误差收敛是至关重要的。
采用重要性采样还可以限制梯度的大小,这对于深度网络的更新是十分有利的。深度网络的更新步长一般不能设置太大,而采用优先经验回放进行更新时,会明显增加高 TD 误差的经验用于网络更新的几率,这样会使深度网络的更新不稳定。采用重要性采样后,网络更新的梯度会受到限制。
为了提高算法模型训练的稳定性,通常让 $\omega$ 除以 $1 / max_i \, \omega_i$ 进行标准化,保证梯度更新可以受到限制。
所以最终重要性采样的权重计算公式如下:
2.4 PER 伪代码
综合“衡量经验优先级的标准”,“随机优先方法”和“重要性采样补偿偏差”,得到优先经验回放的算法伪代码如下:
注意伪代码中没有写出随机优先回放的技巧,不过具体实现中是要用到的。另外也没有说明当经验回放池满了之后怎么执行替换操作。有两种实现方式,一种是把优先级最低的经验给替换掉,另一种是轮流替换到每个位置。
3. 实现细节
3.1 PER 具体实现相关细节
我们不能只根据优先级对所有经验回放样本进行排序来实现优先经验回放。这样做对经验样本插入的时间复杂度为 $O(nlogn)$,采样过程的时间复杂度为 $O(n)$,因此这个效率并不高。需要另外引入一些数据结构来减小时间和空间复杂度。
上面 2.2 节提到对于经验优先级 $p(i)$ 的定义有两种方式,一种称为“排名优先级” (Rank-based prioritization),另外一种称为“比例优先级” (Proportional prioritization)。下面对这两种定义给出具体的实现细节。(其实论文对于这部分的介绍比较笼统,建议直接看代码)
3.1.1 Rank-based prioritization 实现细节
采用基于数组的二叉堆实现的优先队列来存储经验。运行时间上的改进来自于避免对采样分布的分区进行过多的重新计算。(这里论文并没有介绍很多)
3.1.2 Proportional prioritization 实现细节
在这里使用的是 “sum-tree” 数据结构,它是二叉树,每个节点最多只有两个子节点。 每片树叶存储每个样本的优先级, 每个树枝节点只有两个分叉, 节点的值是两个分叉的和,那么根节点的值就是所有优先级的总和 $p_{total}$。这种数据结构给优先级的累计和的计算带来便利,插入(更新树)和采样的时间复杂度降为 $O(log N)$。
3.2 采样细节
假设需要从经验池中抽取 $k$ 个经验($minibatch = k$),首先将累积优先级范围 $[0, p_{total}]$ 等划分为 $k$ 个序列,然后在每个序列中进行均匀随机采样,最后将对应的经验从数据结构中剥离出来。
3.3 $SumTree$ 实现细节
优先经验回放池的数据结构分为三块内容:树的节点索引、节点数据、以及一个单独存放经验的结构。
$SumTree$ 是一种树形结构, 每个叶子存储每个样本的优先级。每个父节点只有两个分支, 父节点的值是两个分支的和, 所以 $SumTree$ 的顶端就是所有优先级的和,如下图所示。
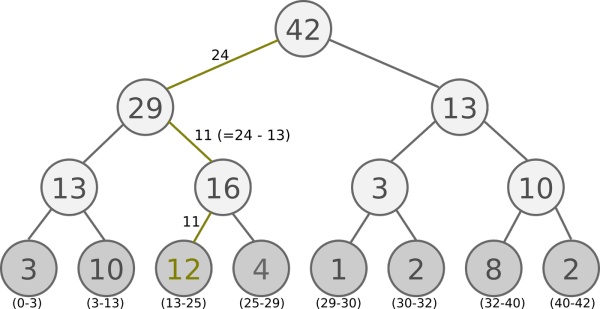
可以发现,叶结点的个数等于之前所有层的节点加起来再加1,设叶结点个数为 $N$,则整棵树的大小为 $2 * N - 1$。
另外还有一个数组(称为 $Data$ 结构)存储所有经验,相当于经验池。$Data$ 结构如下图所示:
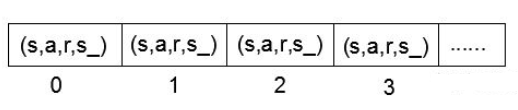
注意 $SumTree$ 树和 $Data$ 数组存储的东西不一样,前者存储的是优先级,后者存储的是经验($transition$)。存储优先级的时候是从 $SumTree$ 的叶子节点开始的,其索引是从 $N - 1$ 开始。而这个优先级对应的经验在 $Data$ 数组中的存储是从 $0$ 开始的,可以看出优先值和对应的经验的索引差为 $N - 1$。
从经验池抽样时, 我们会将优先级的总和除以 $batchsize$(设为 $k$), 分成 $k$ 那么多区间,每个区间的优先级变化范围是
假设如图将所有节点的优先级加起来是 $42$ 的话, 我们需要抽 $6$ 个样本, 这时的区间拥有的优先级是这样:
$[0-7]$,$[7-14]$,$[14-21]$,$[21-28]$, $[28-35]$, $[35-42]$
然后在每个区间里随机选取一个数 $s$,从根节点开始比较,即 $idx=0$,如果左边的子节点比 $s$ 大,则走左边子节点这条,如果左边子节点小于 $s$,则走右子节点,但 $s$ 值要减去左子节点的数值,按照这个规则,一直找到叶结点,返回其索引,以及对应的优先级,还有从 对应的经验。
比如在区间 $[21-28]$ 里选到了 $24$, 就按照这个 $24$ 从最顶上的根节点开始向下比较. 首先看到根节点下面有两个子节点, 左边的子节点 $29$ 比 $24$ 大,所以走左边那条路。接着再对比 $29$ 下面的左边那个点 $13$, 这时 $13$ 比选中的 $24$ 小, 那我们就走右边的路, 并且将手中的值减去 $13$, 变成 $24-13=11$。接着拿着 $11$ 和 $16$ 左下角的 $12$ 比, 结果 $12$ 比 $11$ 大, 那我们就选 $12$ 当做这次选到的优先级,并且可以知道 $12$ 这个节点在树中的索引为 $9$,并且叶子节点的总数 $N = 8$,所以对应的经验在 $Data$ 经验池的索引为 $9 - (N - 1) = 2$。因此从 $Data$ 经验池中顺序取出第三个经验。
从上面 $SumTree$ 的结构图中我们可以注意到,第三个叶子节点优先级最高,它覆盖的采样区间为 $13-25$,也是最长的,因此会比其他节点更容易被采样到。