1. ACER 概念
ACER 就是将 Actor-Critic 和 experience replay 结合起来的强化学习方法。本文 [1] 提出了几种新的技术:带偏差纠正的截断重要性采样、随机 dueling 网络结构、一种新的置信域策略优化方法。
提出 ACER 的概念源于智能体与环境交互的代价高昂,需要减少仿真次数,提高数据的样本利用率。ACER 的出现旨在于设计一个稳定的、样本利用率高的 actor-critic 方法。
2. 相关知识
假设可微分策略符号为 $\pi_\theta(a_t|x_t)$,其中 $x_t$ 是状态输入,策略梯度可以表示为:
论文 [2] 的 Proposition 1 提出,可以将 $A^\pi(x_t,a_t)$ 替换为 $Q^\pi(x_t,a_t)$、折扣回报 $R_t$ 或者时间差分 $r_t+\gamma V^\pi(x_t+1)-V^\pi(x_t)$,不会引入偏差,只是四种式子的方差不一样。
通常直接计算折扣回报 $R_t$ 会引入较大的方差,但是只有较小的偏差。而使用函数逼近状态函数则会引入较大偏差,但是只有较小的方差。通过结合 $R_t$ 和函数逼近两种方法,即保证较小偏差也维持固定方差是 ACER 背后的设计思想。
为了对偏差和方差的权衡,A3C 论文中提出了 $k$-step 回报的方法,通过结合 $k$ 步的奖励以及函数逼近来对方差和偏差进行折衷:
重要性采样是离线强化学习方法中常见的技术,用于控制方差和训练的稳定性。假设当前从经验回放池中采样的一段轨迹为 $\{x_0,a_0,r_0,\mu(\cdot|x_0),\cdots,x_k,a_k,r_k,\mu(\cdot|x_k)\}$,其中 $\mu$ 是行为策略,则使用重要性采样因子的策略梯度为:
$\rho_t$ 就是重要性因子:
3. 具体算法
3.1 离散 ACER
重要性采样是离线强化学习方法中常见的技术,用于控制方差和训练的稳定性。假设当前从经验回放池中采样的一段轨迹为 $\{x_0,a_0,r_0,\mu(\cdot|x_0),\cdots,x_k,a_k,r_k,\mu(\cdot|x_k)\}$,其中 $\mu$ 是行为策略,则使用重要性采样因子的策略梯度为:
$\rho_t$ 就是重要性因子:
上面提到的重要性采样虽然不会带来偏差,但是会引来很大的方差,因为式子中包含无界限的重要性因子 $\rho_t$ 的连乘操作。可以对重要性采样因子进行截断,这是一种解决办法。Degris 提出了另一种利用边缘状态函数的方法。
3.1.1 Marginal value function
Degris [3] 提出利用极限分布上的边缘状态函数来逼近策略梯度:
$\beta(x)$ 是行动策略 $\mu$ 的极限分布:$\beta(x) = lim_{t \rightarrow \infty} P(x_t=x|x_0,\mu)$,上式中没有重要性因子的连乘,只需要对边缘重要性因子 $\rho_t$ 进行估计,因此可以降低方差。
3.1.2 Retrace
为了估计 $Q^\pi(x_t,a_t)$,本文使用了 Retrace($\lambda$) [4] 技术。假定一段由行为策略 $\mu$ 采样的轨迹,Retrace($\lambda$) 估计方法可以表示为:
上式的 $\lambda = 1$。其中 $\hat{\rho}_t$ 是截断重要性因子,$\hat{\rho}_t = min\{c,\rho_t\}$,$\rho_t = \frac{\pi(a_t|x_t)}{\mu(a_t|x_t)}$,Q 是当前对 $Q^\pi$ 的估计。在论文 [4] 中一经证明 Retrace 技术拥有较低的方差,并且对于 tabular 强化学习,任意的行为策略都能使目标策略的状态函数收敛。
为了对 $Q$ 进行估计,采用双头输出的卷积网络,一头输出动作状态的估计值 $Q_{\theta_v}(x_t,a_t)$,另一头输出策略 $\pi_\theta(a_t|x_t)$ 。为了获得$g^{marg}$,ACER 采用 $Q^{ret}$ 来估计 $Q^\pi$ 。为了对 $Q_{\theta_v}(x_t,a_t)$ 进行学习,本文利用 $Q^{ret}$ 为目标函数,建立均方差损失函数来对参数 $\theta_v$ 进行学习:
采用 $Q^{ret}$ 有两个好处:一是降低策略梯度的偏差,而是加快 critic 的学习。
3.1.3 bias correction
公式 ($\ref{7}$) 中的边缘重要性因子可能估计比较大,导致训练不稳定。为了更好地降低策略梯度的方差,本文提出一种截断的重要性因子,并引入一个修正项,如下公式所示(公式 ($\ref{7}$) 中的 $\mathbb{E}_{x_t \sim \beta, a_t \sim \mu}$ 简写为 $\mathbb{E}_{x_t,a_t}$):
其中截断重要性因子 $\overline{\rho}_t = \min\{c,\rho_t\}$,$\rho_t=\frac{\pi(a_t|x_t)}{\mu(a_t|x_t)}$。另外关于动作 $a \sim \pi$ 有 $\rho_t(a)=\frac{\pi(a|x_t)}{\mu(a|x_t)}$,并且 $[x]_+$ 表示只有当 $x>0$ 时,$[x]_+ = x$,否则等于 0。
公式 ($\ref{10}$) 的第一项表示策略梯度估计的方差被限制了,第二项表示修正项,保证估计是无偏的。注意到第二项中只有当 $\rho_t(a) > c$ 时偏正项起作用。假设我们选取较大的 $c$ 值,只有当公式 ($\ref{7}$) 中的策略梯度估计方差非常大时,修正项才会起作用。从公式 ($\ref{10}$) 中可以知道第一项截断权重的最大值为 $c$,第二项修正权重的最大值为 1。
本文将修正项中的 $Q^\pi(x_t,a)$ 用神经网络的输出值 $Q_{\theta_v}(x_t,a_t)$ 进行逼近,而第一项依然用 $Q^{ret}$,最终公式 ($\ref{10}$) 变成以下形式,也就是本文提出的带偏差纠正的截断重要性采样技术:
公式 ($\ref{11}$) 带有 Markov 过程的平稳分布的期望,可以通过行为策略 $\mu$ 的采样轨迹来取均值逼近。因此 ACER 的策略梯度逼近公式为:
注意到,当 $c=\infty$ 时,公式 ($\ref{12}$) 就相当于只有第一项,当 $c = 0$ 时,公式 ($\ref{12}$) 就相当于只有第二项。
3.1.4 置信域策略优化
actor-critic 框架的方法经常会出现较大的方差,本文结合 TRPO 中的置信域优化的思想,将 actor-critic 框架和置信域优化结合起来,限制每次更新的幅度。
TRPO 中需要反复求解费舍尔向量乘积,需要非常大的计算量。本文不用像 TRPO 那样约束新策略与旧策略相近,而是通过维护一个平均策略网络,表示旧策略的滑动平均,并且强制更新后的新策略不能偏离这个均值太远。
首先将策略网络分成两个部分,一个是分布类型 $f$,另一个是深度神经网络输出,代表这个分布的统计特性 $\phi_\theta(x)$。也就是说策略可以表示成:$\pi(\cdot|x)=f(\cdot|\phi_\theta(x))$。为了对平均策略网络 $\phi_{\theta_a}$ 进行更新,本文采用软更新的方法,即 $\theta_a = \alpha \theta_a + (1-\alpha)\theta$ 。
接下来,将公式 ($\ref{12}$) 用 $\phi_\theta$ 表示:
为了进行置信域优化,总共分成两个步骤。
- 解决带 KL 散度约束的优化问题
结合平均策略网络和策略网络,构造二者的 KL 散度约束,如下公式所示:
令 $k = \nabla_{\phi_\theta(x_t)}D_{KL}[f(\cdot|\phi_{\theta_a}(x_t)) | f(\cdot|\phi_\theta(x_t))]$ ,根据 KKT 条件和拉格朗日乘法,很容易解得 $z$ 的最优值为:
公式 ($\ref{14}$) 的约束可以理解为策略梯度的变化量不能超过范围 $\delta$,$k$ 表示策略梯度变化率,$z$ 表示策略梯度。
如果约束满足,则策略梯度没有产生任何改变。否则策略梯度沿着 $k$ 的方向降低变化。
- 后向传播
$z^$ 是关于 $\phi_{\theta}$ 的最优策略梯度,根据链式传播原则,神经网络中的参数可以通过后向传播更新:$\frac{\partial \phi_\theta(x)}{\partial \theta} z^$ 。
3.1.5 伪代码

从主算法中可以看出,先采用 ACER on-policy 算法,然后再根据回放比进行 $n$ 次 ACER off-policy 算法。
注意算法 2 中有一处的赋值 $\mu(\cdot|x_i) \leftarrow f(\cdot|\phi_{\theta’}(x_i))$,应该是作者在ACER on-policy 算法中故意让行为策略等于目标策略。要么就是笔误,右侧可能是 $f(\cdot|\phi_{\theta_a}(x_i))$ 。不过无所谓,问题不大。
3.2 连续 ACER
本文在连续的动作空间对 ACER 做了两次修改,分别在策略估计和置信域优化两个方面。
3.2.1 策略估计修改
Retrace 技术只学习了 $Q_{\theta_v}$,没有学习 $V_{\theta_v}$。作者觉得二者合一对状态的估计更加准确,方差更小。
本文设计了一种称为 Stochastic Dueling Networks 的网络结构,简称 SDNs,可以同时估计 $V^\pi$ 和 $Q^\pi$ 。网络的输出 $\tilde{Q}_{\theta_v}$ 是对 $Q^\pi$ 的随机估计值,另一个输出 $V_{\theta_v}$ 是对 $V^\pi$ 的确定估计值。$\tilde{Q}_{\theta_v}$ 的计算可以通过 $V_{\theta_v}$ 表示:
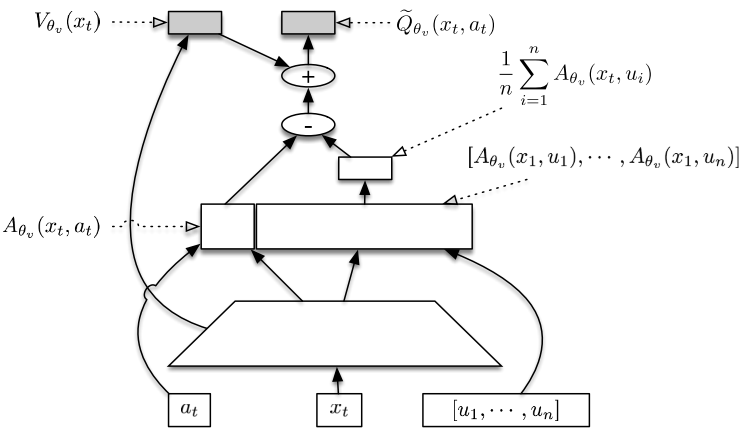
同时还可以依据 $\tilde{Q}_{\theta_v}$ 和目标 $Q^{target}$ 间的差距来更新 $V_{\theta_v}$ 和 $V^{target}$。也就是说在某种意义上 $\tilde{Q}_{\theta_v}$ 和 $V_{\theta_v}$ 的更新是一致的。这种一致性可以通过以下两个等式来说明:
本文通过推导,利用带修正项的重要性截断技术的形式,推导出一种新的 $V^{target}$ 表达形式(推导过程见文章附录 D):
最后本文在更新 $Q^{ret}$ 的参数时采用的截断重要性因子 $\overline{\rho}_t$ 也加了一点改变:
其中 $d$ 是动作空间的维度。这个改变只是工程性的,并没有理论的意义。
3.2.2 置信域优化修改
连续情况下的策略梯度更新公式与离散情况下的策略梯度更新公式相似,除了将公式 ($\ref{12}$) 中的 $Q^{ret}$ 替换为 $Q^{opc}$ 。$Q^{opc}$ 的计算公式与 $Q^{ret}$ 非常相似,除了截断重要性因子被替换为 1 [5]。连续情况下的策略梯度公式如下所示:
公式 ($\ref{20}$) 的期望形式可以用蒙特卡罗方法代替,最终写成:
$Q^{opc}$ 出自另一篇研究异策略纠正的论文 [5],可以发现它的形式与 Retrace 技术中的 $Q^{ret}$ 非常像,除了没有截断重要性因子。论文 [5] 中分析,由于没有截断重要性因子,训练过程 $Q^{opc}$ 比 $Q^{ret}$ 不稳定,并且不适用于策略评价(policy evaluation)过程。但是恰恰由于没有截断重要性因子,$Q^{opc}$ 会更好地保留回报(return)的信息,从而在策略梯度中更好地估计 $Q^\pi$,加快训练过程。用一句话概括就是,$Q^{opc}$ 不适用于策略评价(policy evaluation)过程,但适用于策略提升(policy improvement)过程。
3.2.3 伪代码

伪代码中有几个细节需要注意:
- 首先这是一个 off-policy 的方法,不像离散版本中既结合了 on-plicy,也结合了 off-policy。
- 其次,$a_i$ 和 $a_i’$ 代表的意义不同,准确来说,代表的采样时刻不同。$a_i$ 是存储在回放池中的,也就是在仿真时刻所执行的动作。而 $a_i’$ 是在策略更新的时刻,根据当前的目标策略 $f(\cdot|\phi_{\theta’}(x_t))$ 所采样的。
- 最后就是注意 $\rho_i$,$\rho_i’$ 和 $c_i$ 三种重要性因子的使用。 $\rho_i’$ 是用于策略梯度的偏差修正。
4. 工程设置
4.1 ATARI 环境
网络结构:第一层为 32 个 $8 \times 8$ 步长为 4 的滤波器,第二层为 64 个 $4 \times 4$ 步长为 2 的滤波器,第三层为 64 个 $3 \times 3$ 步长为 1 的滤波器,最后一层为 512 个单元的全连接层。每个隐藏层都采用非线性激活函数。网络输出为 softmax 策略和 Q 值。
超参数:熵正则化项权重为 0.001,奖励折扣因子为 $\gamma=0.99$,每隔 20 个步长更新一次,即 $k=20$。截断重要性权重超参数 $c=10$,置信域优化约束上限 $\delta=1$,软更新系数 $\alpha=0.99$。
4.2 Mujoco 环境
网络结构:和 ATARI 环境相同的网络结构,网络输出为策略和状态值。另外还维护一个小型的网络,输出为随机的优势值 $A$,更新也是利用目标 $Q^{target}$ 和 $V^{target}$ 的更新公式。
超参数:SDNs 中的超参数(公式 ($\ref{16} $) )中的 $n$ 取值为 5。奖励折扣因子为 $\gamma=0.995$,每隔 50 个步长更新一次,即 $k=50$。截断重要性权重超参数 $c=5$,软更新系数 $\alpha=0.99$。策略分布采用高斯分布,固定标准差为 0.3。学习率从范围 $[10^{-4},10^{-3.3}]$ 中 log-uniformly 采样。置信域优化约束上限 $\delta$ 从范围 $[0.1,2]$ 中均匀采样。总共采样出 30 组超参数设置。
参考文献
[1] Wang, Z., Mnih, V., Bapst, V., Munos, R., Heess, N., Kavukcuoglu, K., & De Freitas, N. (2019). Sample efficient actor-critic with experience replay. 5th International Conference on Learning Representations, ICLR 2017 - Conference Track Proceedings, (2016).
[2] Schulman, J., Moritz, P., Levine, S., Jordan, M., & Abbeel, P. (2015). High-Dimensional Continuous Control Using Generalized Advantage Estimation. 1–14. Retrieved from http://arxiv.org/abs/1506.02438
[3] Degris, T., White, M., & Sutton, R. S. (2012). Off-policy actor-critic. Proceedings of the 29th International Conference on Machine Learning, ICML 2012, 1, 457–464.
[4] Munos, R., Stepleton, T., Harutyunyan, A., & Bellemare, M. G. (2016). Safe and efficient off-policy reinforcement learning. Advances in Neural Information Processing Systems, (Nips), 1054–1062.
[5] Anna Harutyunyan, Marc G Bellemare, Tom Stepleton, and Remi Munos. Q (λ) with off-policy corrections. arXiv preprint arXiv:1602.04951, 2016.