Haarnoja, T., Zhou, A., Abbeel, P., & Levine, S. (2018). Soft actor-critic: Off-policy maximum entropy deep reinforcement learning with a stochastic actor. 35th International Conference on Machine Learning, ICML 2018, 5, 2976–2989.
1. 论文概要
无模型的强化学习算法存在采样复杂度高和收敛性弱的问题。即使很简单的任务,所需要的样本数量都达到上百万。另外对于不同问题,这些强化学习算法的超参数需要精细调整。本文提出一个 soft actor-critic 强化学习方法,是就基于最大化熵的 off-policy 强化学习方法。在这个框架中,actor 旨在于最大化奖励回报和熵。本文提出的算法在稳定性和性能方面都胜过目前的强化学习算法。
之所以 TRPO、PPO 和 A3C 这些算法的采样复杂度高,是因为他们都需要在每个梯度更新步骤采集新的样本。而 off-policy 方法一般用在 Q-learning 一类强化学习方法上,与传统的策略梯度方法结合会导致算法稳定性和收敛性下降。另外,最大化熵方法通常能提高探索效率和鲁棒性,但还没有与 off-policy 和 policy-gradient 等强化学习模型结合起来。
本文的主要贡献点就是将 off-policy 和最大化熵方法结合到 ac 框架中,用于连续空间的控制任务,并将算法命名为 SAC (soft actor-critic)。之前的很多 AC 框框架只采用了 on-policy 方法,并只是将熵当作正则项。
2. 相关知识
传统的强化学习目标是 $\sum_t \mathbb{E}_{(s_t,a_t)\sim \rho_\pi}[r(s_t,a_t)]$,在此基础上添加了策略的熵作为目标项:
超参数 $\alpha$ 控制着熵这一项的重要程度,也就是控制着策略的随机程度。对于无限时长的任务,可以加入折扣因子:
3. 算法推导
3.1 Soft Policy Iteration
本文先将最大熵方法和策略迭代方法结合得出收敛性结论(针对 tabular-setting)。
首先定义 soft 策略迭代中的 soft 策略评估过程,假设 $\mathcal{T}^\pi$ 为修改后的贝尔曼操作子,定义 soft 策略评估过程如下:
以上公式的 $V(s_t)$ 称为 soft 状态函数,其中融合了 $\pi$ 的熵。根据公式 $\eqref{3}$ 可以证明以下引理。
引理 1:考虑公式 $\eqref{3}$ 中的 $\mathcal{T}^\pi$,并给出一个映射:$Q^0:\mathcal{S}\times \mathcal{A} \rightarrow \mathbb{R}, |\mathcal{A}|< \infty$,定义 $Q^{k+1}=\mathcal{T}^\pi Q^k$。当 $k \rightarrow \infty$ 时,$Q^k$ 将会收敛为 $\pi$ 的 soft Q-value 。
引理 1 的结果表示公式 $\eqref{3}$ 定义的贝尔曼方程可以收敛。引理 1 在本文的附录 B.1 中有证明。
接下来定义 soft 策略迭代中的 soft 策略提升过程:
公式 $\eqref{4}$ 中的 $\pi’ \in \Pi$ 表示将策略限制在一个范围中,者可以对应为某些分布家族的参数化。为了实现限制 $\pi \in \Pi$,本文采用 KL 散度进行投影的方式,也就是公式 $\eqref{4}$ 中出现的 $D_{KL}$ 。另外 $Z^{\pi_{old}}(s_t)$ 是配分函数,用来归一化分布,实际上是不可计算的,但是对新策略的参数求导没有贡献,因此可以忽略。根据公式 $\eqref{4}$ 可以证明以下引理。
引理 2:令 $\pi_{old} \in \Pi$,并令 $\pi_{new}$ 为公式 $\eqref{4}$ 的结果,那么 $Q^{\pi_{new}}(s_t,a_t) \ge Q^{\pi_{old}}(s_t,a_t), \forall (s_t,a_t) \in \mathcal{S} \times \mathcal{A}, |\mathcal{A}| <\infty$
引理 2 的结果表示公式 $\eqref{4}$ 定义的策略提升过程能满足新策略的性能不下降。证明过程在本文的附录 B.2 。
根据引理 1 和引理 2 的结论,本文证明了以下定理(证明过程在本文的附录 B.3)。
定理 1:重复运用 soft 策略评估和 soft 策略提升,最终可以收敛到最优策略 $\pi^*$,使得 $Q^{\pi^*}(s_t,a_t) \ge Q^\pi(s_t,a_t),\forall \pi \in \Pi \;\; and (s_t,a_t) \in \mathcal{S} \times \mathcal{A},|\mathcal{A}|<\infty$ 。
3.2 Soft Actor-Critic
以上的 soft policy iteration 方法只是针对离散的状态和动作空间。为了应对大规模的连续状态和动作空间,需要对状态函数和策略进行函数逼近,也就是参数化。
本文总共对三个函数进行了参数化:soft 状态函数 $V_\psi(s_t)$、soft Q 函数 $Q_\theta(s_t,a_t)$,策略函数 $\pi_\phi(a_t|s_t)$ 。对应的参数分别是 $\psi$、$\theta$ 和 $\phi$ 。
根据公式 $\eqref{3}$ ,sot 状态函数是可以通过 soft Q 函数和策略函数来计算的,但是引入一个单独的函数估计可以提高训练的稳定性,以及便于与其他网络同时训练。
soft 状态函数的训练目标是:
这里的 $\mathcal{D}$ 表示经验回放池。注意公式 $\eqref{5}$ 中的 $a_t$ 不是从经验回放池中抽取的动作,而是从当前策略采样的动作。
公式 $\eqref{5}$ 求导可得:
soft Q 函数的训练目标是:
其中:
公式 $\eqref{7}$ 求导可得:
其中 $V_\bar{\psi}$ 表示的是独立的目标网络,参数 $\bar{\psi}$ 的更新是通过 $\psi$ 进行 soft update,也就是滑动加权平均。
最后是策略的训练目标:
为了对策略进行参数化,本文利用神经网络加噪声的形式表示:$a_t = f_\phi(\epsilon_t;s_t)$,其中 $\epsilon_t$ 表示输入噪声向量,可以从某些固定分布中采样。重新策略的训练目标为:
联合公式 $\eqref{3}$ 对公式 $\eqref{11}$ 进行求导得:
最终 SAC 的伪代码如下:

4. 消融实验
4.1 Stochastic vs. deterministic
deterministic SAC 不加入熵作为目标,同时策略函数输出的策略是固定的,没有加入噪声。对比结果如下:
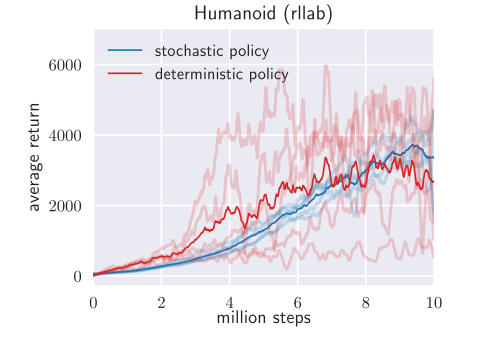
4.2 reward scaling
reward scaling 可以认为是调整公式 $ \eqref{1}$ 中的超参数 $\alpha$,只不过是通过放大奖励项的倍数,$\alpha$ 的值则设为 1。对比结果如下:
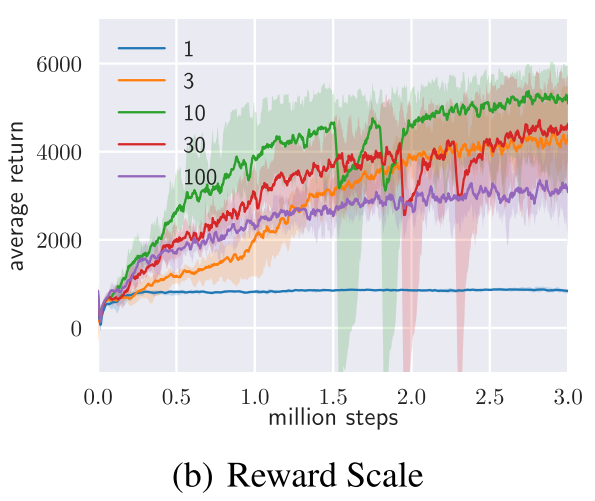
4.3 target smoothing coefficient
就是指目标状态网络的软更新超参数 $\tau$ 的取值,对比结果如下:
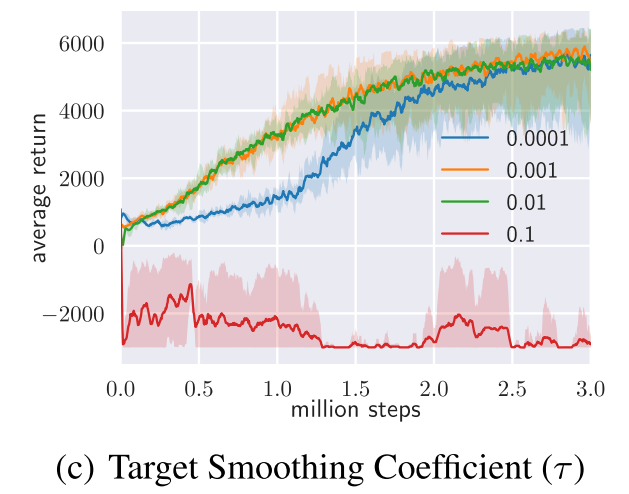
4.4 hard update vs. soft update
目标网络的更新还可以采用硬更新方法,就是每隔一段训练周期,就将行为网络的参数赋值给目标网络。对比结果如下:
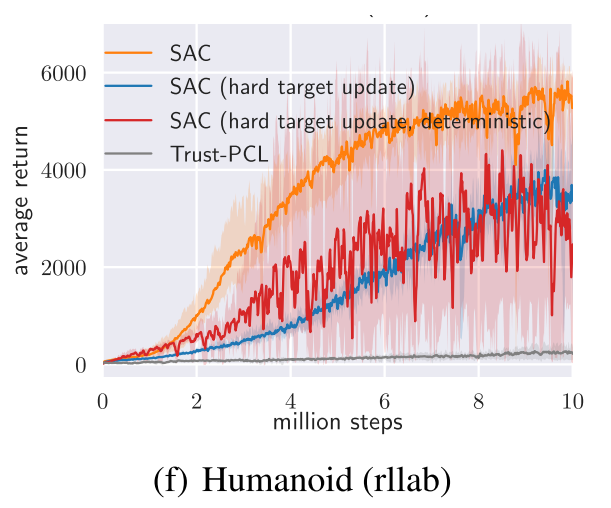
5. 工程设置
